Ghost bands
The separation of core electrons from valence electrons in the FLAPW method relies on the orthogonality of the LAPW basis to the core electron states. This is only given if the core electron states vanish in value and slope at the MT sphere boundary. In reality this is only approximately fulfilled and if the system under investigation strongly deviates from this assumption one obtains (bad) representations of core electron states with the LAPW basis. These representations are bad since the energy parameters are typically far from the core electron eigenenergies. They are called ghost bands. An example for such a ghost band can be seen in figure 1.
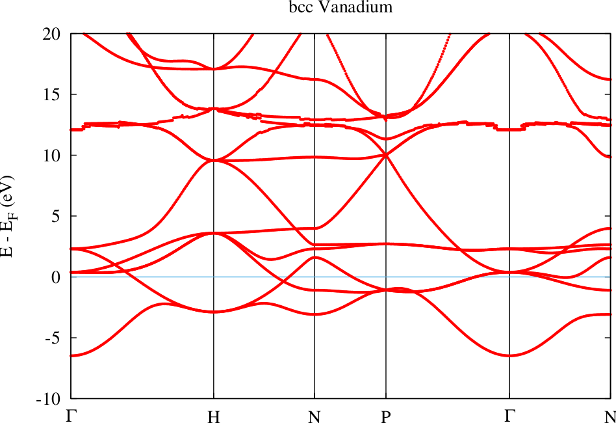
The example shows the band structure of bcc Vanadium. In the calculation all electrons up to the states were treated as core electrons, all other electrons as valence electrons. Between 10 and 15 eV above the Fermi energy a strange band with nearly no dispersion can be observed. Since the energy of this band shows sudden variations with the k point it is clear that the respective representation is rather bad. These sudden variations are due to small differences in the basis set size for the different k points. The effect of these variations can only be so strong if the representation of the band leaves a lot of room for improvement. The vanishing dispersion of the band is a typical property of ghost bands.
Figure 2 shows the effect of reducing the MT radius in such a case. The obvious effect of such a change is the increase of the number of core electrons reaching out of the MT sphere. This implies that the orthogonality assumption is even less fulfilled. It also implies that the linearization error in the MT sphere becomes smaller since the part of the basis functions that is constructed in with the energy parameters fills a smaller fraction of space.
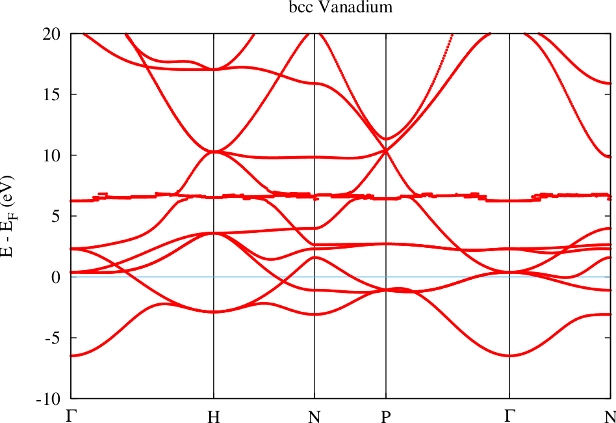
In the band structure the reduction of the MT radius shows up in a lowering of the energy of the ghost band to about 6 eV above the Fermi energy.
The effects of a further reduction of the MT radius are shown in figure 3. Now the ghost band is only about 4 eV above the Fermi energy.
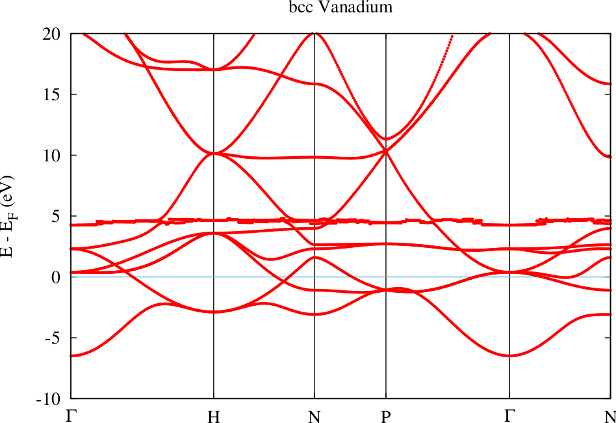
Reducing the MT radius even further results in a crash of the calculation. This is because the ghost band starts to become occupied in the construction of the charge density and therefore contributes to the potential. Since the respective state is already occupied in terms of core electrons this leads to a double-occupation resulting in a messed up potential. The potential then can not be used any more to determine meaningful the energy parameters and/or core electron states. Fleur detects this and therefore stops the calculation. In this example the error message indicates that the Dirac equation can not be solved any more, but other error messages are also possible and this error can also have other causes. It may also be that no error message appears and only the result is wrong.
The number of core electrons reaching out of the MT sphere is a good indicator to judge whether there may be problems due to ghost states in the calculation. For SCF calculations numbers below are typically safe territory, for numbers above the validity of the calculation should strongly be investigated in detail.
The number of core electrons reaching out of each MT sphere can be extracted from the out.xml file
by invoking grep lostElectrons out.xml.
Note that certain calculations may need a high-quality representation of the unoccupied states, too. In such a case the orthogonality requirements may have to be fulfilled to an even higher degree.
The common approach to deal with semicore states leading to ghost bands is to remove them from the core electrons and treat them as valence electrons. The first step in this procedure is the identification of the responsible states. A good indicator for this are the energy eigenvalues of the core electron states. Those states featuring the highest eigenenergies most probably reach farthest out of the MT sphere.
In the out.xml file the energy eigenvalues of the core electrons for each atom type are provided
within the respective coreStates element. Also the number of electrons lost from the core are provided here.
An example for this output for the discussed Vanadium is shown below. The and core electron states
feature the highest eigenenergies.
<coreStates atomType=" 1" atomicNumber=" 23" spin="1"
kinEnergy=" 941.0636778793" eigValSum=" -550.9805159504"
lostElectrons=" 0.111893">
<state n="1" l="0" j="0.5" energy="-195.9388108744" weight="2.000"/>
<state n="2" l="0" j="0.5" energy="-21.4169509005" weight="2.000"/>
<state n="2" l="1" j="0.5" energy="-17.9790788510" weight="2.000"/>
<state n="2" l="1" j="1.5" energy="-17.7189379876" weight="4.000"/>
<state n="3" l="0" j="0.5" energy="-1.8913495403" weight="2.000"/>
<state n="3" l="1" j="0.5" energy="-0.9625902671" weight="2.000"/>
<state n="3" l="1" j="1.5" energy="-0.9318007834" weight="4.000"/>
</coreStates>
For the representation of the semicore electron as a valence electron also the representation of the respective state by the valence basis has to be improved. This is done by adding a local orbital (LO) for the representation of this state to the LAPW basis. The outcome of the treatment of the electrons as valence electrons with an adapted LO is shown in figure 4.
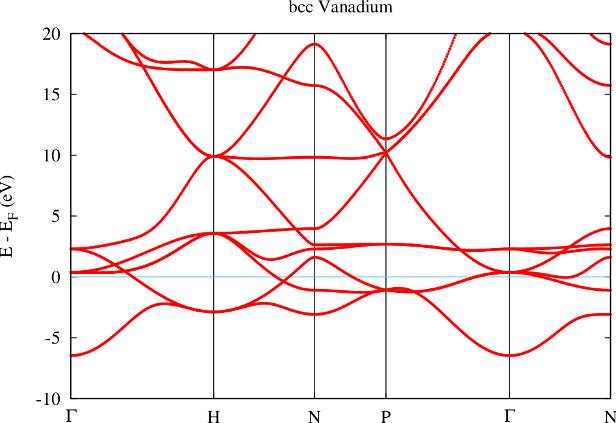
From the band structure obtained with the semicore LO it is directly visible that the ghost band is gone. With the LO the representation of the semicore state is good enough to put it energetically to the place where it belongs: Far below the valence band.
If the extension of the basis with LOs is not an option one may also change the MT radii such that less electrons reach out. However, this is cumbersome since the effect is small and one may end up with overlapping MT spheres, which is not allowed.
