Spin spirals
Often the magnetic ground state in a material is neither ferromagnetic nor antiferromagnetic but a noncollinear magnetic structure. In this example we will investigate a special case of such a noncollinear magnetic structure in fcc Fe: A spin spiral in z-direction, where the magnetization rotates in the xy plane.
It is obvious that the FM and AFM states are special cases of such spin spirals. In the FM case the rotation vanishes and in the AFM case the rotation from one atomic layer to the next is . The exception here is that in Fleur a spin-spiral calculation assumes, according to the provided angles, a collinear orientation of the magnetization within the MT spheres, while in the interstitial region the magnetization direction varies in spaces.
Fleur can efficiently describe such spin spirals by employing the generalized Bloch theorem. It allows us to describe the FM and AFM configuration, as well as all other magnetic configuration covered by such a spin spiral in a unit cell with a single Fe atom.
In the FeSpinSpiral directory the inpFeSpinSpiral.txt is a starting point for such a calculation. Change into that directory and display the file.
cd FeSpinSpiral/ ; cat inpFeSpinSpiral.txt
fcc Fe, Cu lattice constant, spin-spiral setup, single atom unit cell
&lattice latsys='fcc' a=6.82 /
1
26 0.0 0.0 0.0
&qss 0.3 0.3 0.0 /
It describes a primitive fcc unit cell. The &qss entry is the spin-spiral vector q associated with the general expression for the magnetization in the MT spheres
where is the lattice vector pointing from the origin to unit cell , is the position of atom in the unit cell, is the cone angle between the magnetic moment of atom and the rotation axis, and is an atom-dependent phase shift.
Multiplying the q vector with the reciprocal Bravais matrix shows that it actually describes a spin spiral in z direction. With the expression for the magnetization then descibes the FM state for and the AFM state for for .
Specifying the spin-spiral vector in the inpgen input is important because of two reasons:
- Spin spirals break the symmetry of the chemical unit cell. If it would not be specified in the inpgen input it may be incompatible to the found symmetry operations.
- Normally inpgen does not write out the parametrization for calculations involving noncollinear magnetism. This is only done if inpgen is invoked with the
-nococommand line switch or a spin spiral is specified in the inpgen input. Specifying the spin spiral here will also set a few switches in the Fleur input file to special valus./calculationSetup/magnetism/@l_nocoand/calculationSetup/magnetism/@l_ssare set to"T"to activate the spin-spiral calculation and/calculationSetup/coreElectrons/@ctailis set to"F"because this feature is not implemented for calculations with noncollinear magnetism.
Generate the Fleur input file.
inpgen -f inpFeSpinSpiral.txt
Before starting the spin-spiral calculation we have to perform a few more modifications in the Fleur input file:
- To reduce the computational demands we use a reduced k-point mesh with points. We generate it by invoking
inpgen -inp.xml -kpt grid=8,8,8
- Set
/calculationSetup/scfLoop/@itmaxto"50". (This is again unproblematic in this special case.) - Select the new k-point mesh by setting
/cell/bzIntegration/kPointListSelection/@listNameto"default-3". - Specify of the spin spiral by setting
/atomGroups/atomGroup/nocoParams/@betato"0.5*Pi".
We will calculate spin spirals of the form for qXY from 0.0 to 0.5 in steps of 0.1. For this create directories qXY-0.0 to qXY-0.5. Copy all xml files needed for these calculations to each of the directories.
mkdir qXY-0.0 ; mkdir qXY-0.1 ; mkdir qXY-0.2 ; mkdir qXY-0.3 ; mkdir qXY-0.4 ; mkdir qXY-0.5
cp *.xml qXY-0.0/ ; cp *.xml qXY-0.1/ ; cp *.xml qXY-0.2/ ; cp *.xml qXY-0.3/ ; cp *.xml qXY-0.4/ ; cp *.xml qXY-0.5/
In each directory modify the q vector of the spin spiral in the inp.xml file by adjusting the numbers in /calculationSetup/magnetism/qss, i.e., from
<qss>.0000000000 .0000000000 .0000000000</qss>
to
<qss>.5000000000 .5000000000 .0000000000</qss>
Invoke Fleur in each qXY directory.
cd qXY-0.0 ; fleur_MPI ; cd -
cd qXY-0.1 ; fleur_MPI ; cd -
cd qXY-0.2 ; fleur_MPI ;cd -
cd qXY-0.3 ; fleur_MPI ;cd -
cd qXY-0.4 ; fleur_MPI ;cd -
cd qXY-0.5 ; fleur_MPI ; cd -
Extract the total energy for the self-consistent solution of each calculation, e.g, by invoking
for f in $(find . -name "out"); do grep -H "total energy" $f | tail -1; done
(Note: the outputs might not be properly ordered)
Order the entries and store them in a two-column file with columns containing qXY and the total energy, respectively. Plot the file, e.g., with gnuplot. Your result should look similar to every 2nd point from the following plot.
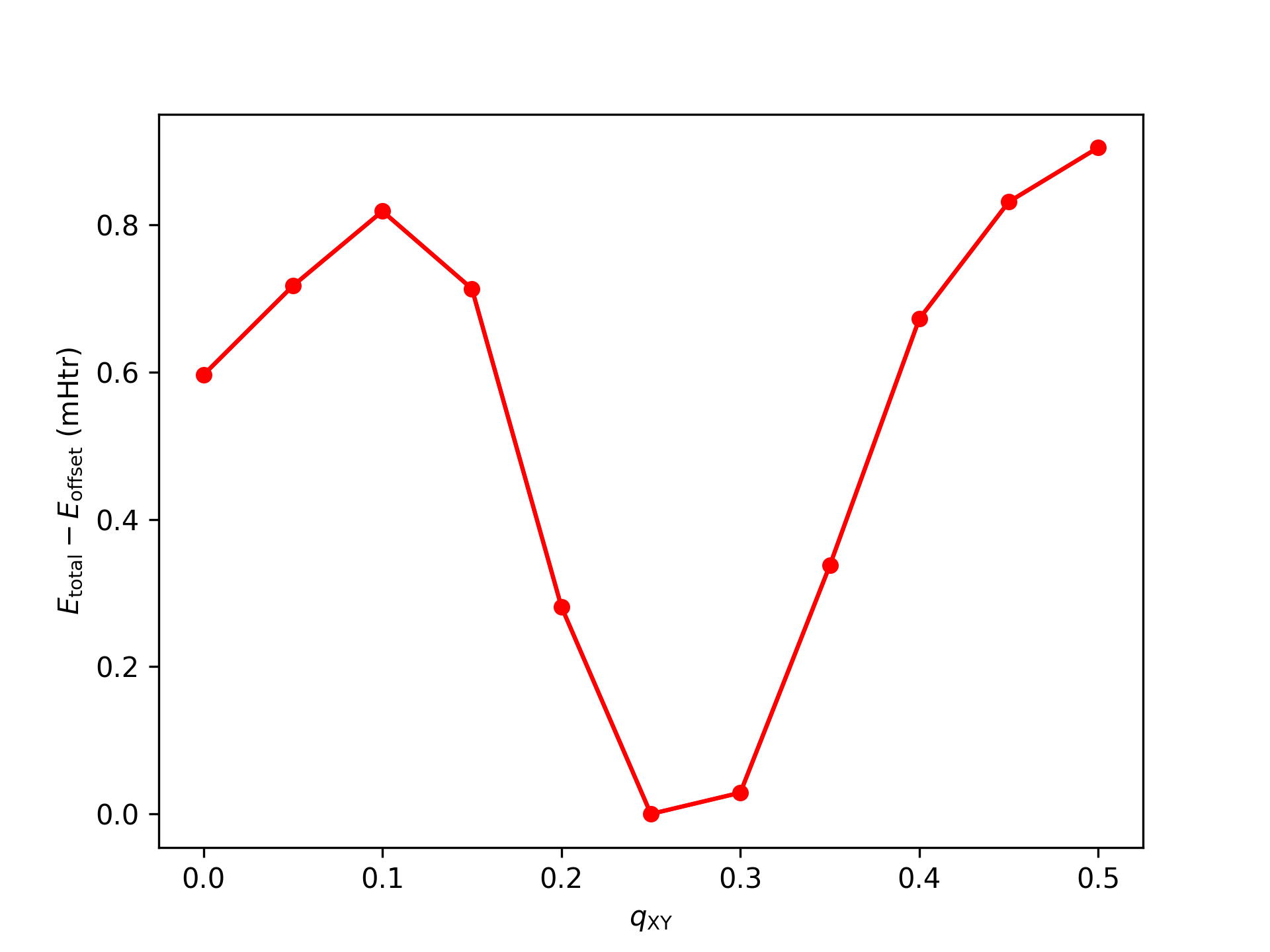
Spin-spiral dispersion for fcc Fe.
While the calculations agree nicely with the previous exercise on the energy difference between FM and AFM configurations, they also show that there is a spin-spiral configuration with between and featuring a lower total energy.
