Treatment of valence electrons
The LAPW basis
The valence electrons are represented by the LAPW basis. It consists of the functions:
A sketch of an LAPW basis function is shown in figure 1.
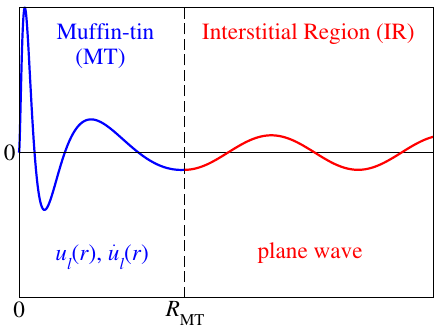
For each sampled -point of the irreducible wedge of the Brillouin zone each LAPW basis function is indexed by the reciprocal lattice vector entering the equation in the plane wave in the interstitial region. A cutoff parameter defines which plane waves are considered in the LAPW basis.
In the input file the reciprocal plane-wave cutoff parameter is specified in units of (calculationSetup/cutoffs/@Kmax).
The MT part of the basis consists of a linear combination of the radial functions and times spherical harmonics . Here is the position relative to atom at and is a composite index for the angular momentum quantum number and the magnetic quantum number . For predefined energy parameters the radial functions are solutions to the radial Schrödinger equation (actually the scalar-relativistic approximation to the Dirac equation) () and their energy derivatives (). The matching coefficients and are automatically calculated by matching the MT part of the LAPW function at the MT boundary in value and slope to the plane wave in the interstitial region. The summation is limited by the cutoff parameters .
In the input file the cutoff parameters can be set for each atom species seperately (atomSpecies/species/atomicCutoffs/@lmax).
As a rule of thumb reasonable values can be obtained from the relation .
The energy parameters are obtained from an automatic procedure within each iteration of the self-consistency loop. By default the Fleur code uses atomic energy parameters, meaning that the energy parameters are obtained as eigenenergies of an artificial atomic problem specified by the radial part of the effective potential within the MT sphere together with an artificial confining continuation of this potential beyond the sphere boundary. For each quantum number up to the shell a main quantum number specifies which eigenenergy becomes the respective energy parameter.
In the input file the main quantum numbers used for the determination of the energy parameters are specified for each -channel up to
(atomSpecies/species/energyParameters). For higher the energy parameter (not the main quantum number) is set to that
of the channel.
The linearization in the LAPW basis allows the accurate representation of Kohn-Sham states within a range of a few eV around the energy parameters. Furthermore one can show that the LAPW basis is orthogonal to core electron states that are completely confined within the MT sphere. This allows to calculate core electron states separately but also within the self-consistent DFT approach.
Local orbitals
Semicore states considerably reach out of the MT spheres but are also rather far away from the valence energy parameters. The user of an FLAPW code has the option to treat such states either as core electrons or as valence electrons. Though, treating them as core electrons can lead to the appearence of ghost bands which may mess up the calculation if they are within the energy range of the occupied bands. If semicore electrons have to be treated as valence electrons the LAPW basis can be extended by local orbitals (LOs) to represent these states.
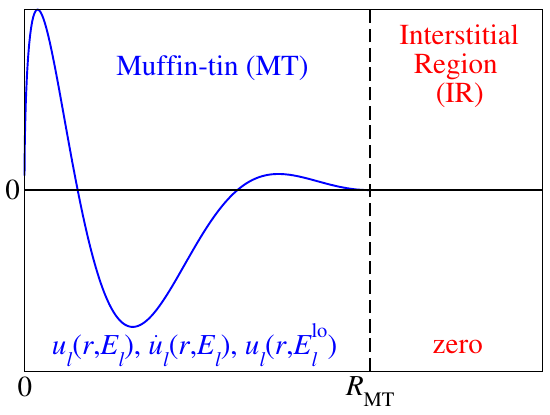
As sketched in the figure above, local orbitals are additional basis functions for a defined channel (one function for each ) that are confined within a MT sphere. They are constructed as: They consist of the already known radial functions and and another radial function . The coefficients , , and are determined by enforcing zero value and slope at the MT sphere boundaries, as well as a normalization of the LO over the MT sphere.
The third radial function can be constructed from different recipies. For the representation of semicore states one typically sets , i.e., one uses a solution to the spherical potential at an energy parameter that is near the semicore state.
LOs can also be used to represent unoccupied states, e.g., by using an energy parameter within the range of these states, or to generally eliminate the linearization error for the valence electrons by setting . The double dot in this expression denotes the second energy derivative.
In the Fleur input file local orbitals can be added for each atom species directly below the specification of the energy parameters in XML elements
atomSpecies/species/lo. See the input file documentation for details on the specification of the third radial function in this XML element.
