The LAPW basis for thin film systems
Calculations on thin films can be performed in different ways. A popular approach to this task is to define a bulk unit cell in which the film is provided along the xy-plane and the width of the film in z direction only covers a small fraction of the unit cell's length in that direction. Such a setup defines periodic repetitions of the film in z direction and one has to make sure that the vacuum in between the films is large enough to decouple them.
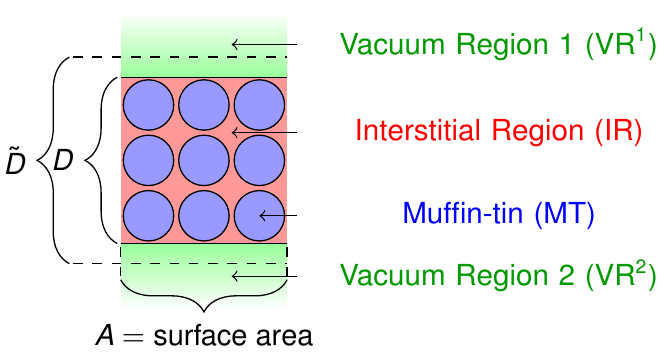
On the basis of the FLAPW method a more elegant treatment of thin film systems is possible. As sketched in the following figure one can set up unit cells with semi-infinite vacuum regions above and below the film.
An LAPW basis function for such a setup is defined as
where the extension in the vacuum regions consists of the two functions and are solutions and energy derivatives to the Schrödinger equation in the respective vacuum region
at the energy parameter . The coefficients and are determined by enforcing continuity of value and slope of the basis function at the vacuum boundary defined by the parameter . The z components of the plane waves in the interstitial region are constructed such that they feature a periodicty in agreement to the parameter . Note that is larger than to avoid a kink of the implicitely periodic interstitial representation of the wave functions at the interstitial-vacuum boundaries.
For film setups the parameters and are specified in cell/filmLattice/@dVac and cell/filmLattice/@dTilda.
For each vacuum the energy parameters are set in the respective cell/filmLattice/vacuumEnergyParameters element for the
spin-up (cell/filmLattice/vacuumEnergyParameters/@spinUp) and spin-down (cell/filmLattice/vacuumEnergyParameters/@spinDown)
channel separately, relative to the vacuum potential at an infinite distance from the film. In the case of a nonmagnetic calculation
the value for the spin-up electrons is used for the calculation of the energy parameter. If both vacua are equivalent only a single
cell/filmLattice/vacuumEnergyParameters element for vacuum 1 is present. It is then also used for vacuum 2.
Be aware that with the automatically determined and one only specifies the thickness of the film, but the film center with respect to the z axis (normal to the film plane) is controlled by the user specified coordinates in the inpgen input. For computational stability and demands it is advisable to construct the film such that it is centered around the plane, or at least features only a limitted displacement (like a single atomic layer) with respect to this ideal condition.
