Treatment of noncollinear magnetism
In the case of noncollinear magnetism, the Kohn-Sham equation obtains the form
where is the unit-matrix. The kinetic energy part of the Hamiltonian is diagonal in the two-dimensional spin space. Only the off-diagonal part of the hermitian potential matrix
couples the two components of the Pauli spinor . It is obtained from the density matrix, , that is given by a very simple relation in terms of the solutions of the Kohn-Sham equation, :
It is related to the density and magnetization by
where is the unit-matrix in spin-space and is the vector of the Pauli matrices.
The parametrization of calculations with noncollinear magnetism requires several optional tags
in the Fleur input file. To generate templates for these tags the input generator should be
invoked with one of the command-line options -noco or -explicit. This will generate
an enhanced magnetism section within the calculationSetup block and further nocoParams
tags in each atomGroups/atomGroup. In the Fleur input file a noncollinear calculation is
activated by setting the calculationSetup/magnetism/@l_noco switch to T.
Note, that in a non-collinear calculation you can monitor the convergence of all
three parts of the density matrix, the two diagonal ones (spin 1 and 2) and one
of the off-diagonals (spin 3). In non-collinear calculations core-tail corrections
have to be switched off: calculationSetup/coreElectrons/@ctail has to be set to F.
When performing calculations with noncollinear magnetism in Fleur the magnetization in the interstitial region is treated as a continuous vector field while in the MT spheres the magnetization is approximated to be collinear and pointing in a fixed direction. Only the magnitude of the magnetization may change within a MT sphere. This is a reasonable approach for transition metals with small spin-orbit effects. The following figure illustrates this approach.
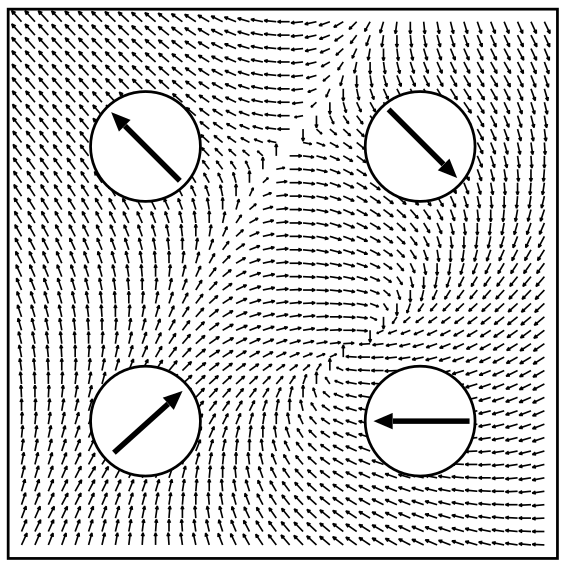
In the Fleur input file the direction of the magnetization in the muffin-tin spheres is specified w.r.t. the global frame for
the representative atom of each atomGroup in the associated enclosed nocoParams tag.
The spin-quantization axis (SQA) is provided by the angles (azimuthal angle similar to in the context of SOC) and (polar
angle similar to ). The example below demonstrates the nocoParams for some atom group with
defined and .
<nocoParams l_relax="F" alpha="Pi/2.0" beta="Pi/4.0"
b_cons_x="0.0" b_cons_y="0.0"/>
Assume that there are two symmetry equivalent atoms in the same atomGroup of a unit cell, then setting
and describes an antiferromagnetic structure.
In detail the angles and define the direction of the exchange field in the atoms at the start of a self-consistency step. After the diagonalization, the resulting charge density is not necessarily collinear in the muffin-tin spheres and even the average magnetization direction can point away from the defined SQA. It can happen (e.g. due to symmetry) that the magnetization stays in the direction of the SQA, but generally this will not be the case.
To consider the full non-collinear output magnetization density (also in the MT spheres) for a plot the
switch calculationSetup/magnetism/mtNocoParams/@l_mperp has to be set to T. Afterwards one has to follow the normal
plotting procedure for a density.
Note that if spin-orbit coupling is considered together with noncollinear magnetism, i.e., calculationSetup/soc/@l_soc is
set to T, spin-orbit coupling is already treated in first variation. In this case calculationSetup/cutoffs/@numbands
is not a relevant cutoff parameter.
Due to a generalization of the treatment of noncollinear magnetism the following calculation modes are not documented correctly.
Besides just keeping the angles and fixed there are two optional calculation modes that deal with output magnetization directions in the MT spheres that do not conicide with the input directions:
- Adjusting the SQA in the direction of the output magnetization
- Constraining the magnetization to the direction of the specified SQA
In both cases, it is necessary to know the component of the output magnetization that is perpendicular to the SQA.
This is obtained by setting calculationSetup/nocoParams/@l_mperp to T.
In the first case, the relaxation of the magnetic moments, it is then sufficient
to set for the respective atom groups atomGroup/nocoParams/@l_relax to T.
After each iteration and are adjusted to the output magnetization,
if the mixing parameter calculationSetup/nocoParams/@mix_b is set to 1.0 completely, for
smaller parameters an intermediate direction is taken (zero means no relaxation). Be aware that
such a relaxation can lead to slow convergence, sometimes it helps to remove the mixing_history from time to time.
For the case of constraining the magnetization one has to set the switch calculationSetup/nocoParams/@l_constr
to T. Then, a constraining field is calculated for each atom
which is then added to the effective field . The
ratio of perpendicular magnetization, and magnetization
along the SQA, , is proportional to the true constraining field
but the value has to be determined self consistently (with being the
mixing factor mix_b).
For each atom group the values of the constraining field are written as atomGroup/nocoParams/@b_cons_x
and atomGroup/nocoParams/@b_cons_y in the inp.xml file for the next iteration.
Treatment of noncollinear magnetism inside the Muffin-tin sphere
Before discussing the setup and usage of this feature please be aware that this feature requires that FLEUR has access to a working hdf5 library.
Generating an input file using the -noco option of the input generator will also genreate some additional nocoParams in
the calculationSetup section. The nocoParams which are relevant for setting up
a calculation which includes noncolinearities inside the Muffin-tin sphere are l_mtNocoPot and l_mperp.
Both of these must be set to T instead of the default F.
Setting the calculationSetup/nocoParams/@l_mtNocoPot switch to T allows offdiagonal elements of the potential inside the Muffin-tin sphere.
As with all noncolinear calculations in FLEUR
calculationSetup/coreElectrons/@ctail has to be set to F.
Furthermore calculationSetup/magnetism/@jspins should equal 2 if the input file has been generated correctly.
Including noncolinearities inside the Muffin-tin sphere is known to be the reason of convergence issues.
We strongly recommend using LDA like funtcionals since GGA like functionals seem to compound the convergence issues.
If GGA like functionals have to be used we recommend first using the Anderson mixing scheme and as soon as convergence problems appear switching to simple mixing.
After finishing an iteration the individual magnetization components (mx, my and mz) of each atom are written in the out file.
Be aware that these values are calculated in the local frame of the atom which is either defined in the input file
by using the angles
atomGroup/nocoParams/@alpha and
atomGroup/nocoParams/@beta or is subject to change if the relaxation feature activated by
calculationSetup/nocoParams/@l_relaxSQA which keeps the z-axis of the local atom frame aligned to the direction of magnetization. If l_relaxSQA="T" the
values of mx, my and mz should remain small at any time of the calculation.
If one wants to know the orientation of the local frame while this feature is activated
one has to take a look at the angles which are written in the out file after each iteration along with the magnetization components.
Those angles are called nococonv%alpha and nococonv%beta and are subject to change if l_relaxSQA is set to T.
Including noncolinear magnetism inside the Muffin-tin sphere into FLEUR calculations is known to work with spin-orbit coupling and local orbitals.
The combination of LDA + U calculations and noncolinearities in the Muffin-tin sphere is possible but to achieve resonable results it is mandatory to set l_relaxSQA="T".
The reason for that is that the LDA + U matrix which is used in FLEUR is always calculated in the local frame.
Therefore the charge density in the Muffin-tin needs to be kept in the same frame.
This is achieved by relaxing the SQA in a way that the local frame of the atom aligns with the magnetization direction.
You can define atomGroup/nocoParams/@alpha and atomGroup/nocoParams/@beta at the beginning of a
FLEUR calculation with l_relaxSQA="T" is set you should set both angles in all atomgroups to 0.0 before restarting the calculation.
This also holds if you want to switch to l_relaxSQA="F" while restarting a calculation. For mixing purposes the charge density is stored unrotated in the cdn/cdn.hdf files.
The usage of spin-orbit coupling in combination with the relaxation l_relaxSQA="T" can cause severe convergence issues. In order to overcome those issues the parameters calculationSetup/nocoParams/@mix_RelaxWeightOffD has been introduced.
The parameter mix_RelaxWeightOffD gives a weight to the magnetization components x and y. Default weight for those components is 1. However if e.g. spin-orbit coupling causes those components to appear suddenly this can cause large rotations of the spin-coordinate frames which is unfavoralbe for convergence.
For sensitive system with large spin-orbit effects we recommend to choose the mix_RelaxWeightOffD parameter in the same magnitude as the usual mixing parameter used for your system.
