Band unfolding
Fleur includes the ability to unfold the band structure (see e.g.
O. Rubel, A. Bokhanchuk, S. J. Ahmed and E. Assmann, Unfolding the band structure of discordered solids: from bound states to high-mobility Kane fermions, Physical Review B 90, 115202 (2014))
of a supercell calculation to the one of a primitive unit cell. This feature is controlled by a seperate flag within the output section.
In this section the size of the supercell has to be specified (in multiples of primitive unit cells).
Unfolding the band structure can only be used when the flag for a band structure calculation (/output/@band) is set.
When the boolean flag /output/unfoldingBand/@unfoldBand is set to T, two band structures are calculated.
The band structure of the provided cell (supercell) and a band structure for the primitive cell, meaning the backfolded band structure, is written out.
Fleur then creates additional output files (band_sc.1, band_sc.2 and band_sc.gp) with the same usage as described for the normal
band structure calculation. The gnuplot file can be used directly to plot the backfolded band structure.
Additionally the information is also written to the banddos.hdf file. There it can be used for other plotting tools.
This allows for additional analysis, for example the combination of band unfolding and band character weight is then possible to plot.
The calculation can only run with a number of points for the band structure that is a multiple of the number of mpi threads. This is checked at the beginning of the calculation, if the associated error message is displayed, please adapt your parallelisation or number of points accordingly.
It follows an example for a diamond supercell with a single A-nitrogen-center defect. The band unfolding specification in the input file for such a calculation is:
<unfoldingBand unfoldBand="T" supercellX="4" supercellY="4" supercellZ="4"/>
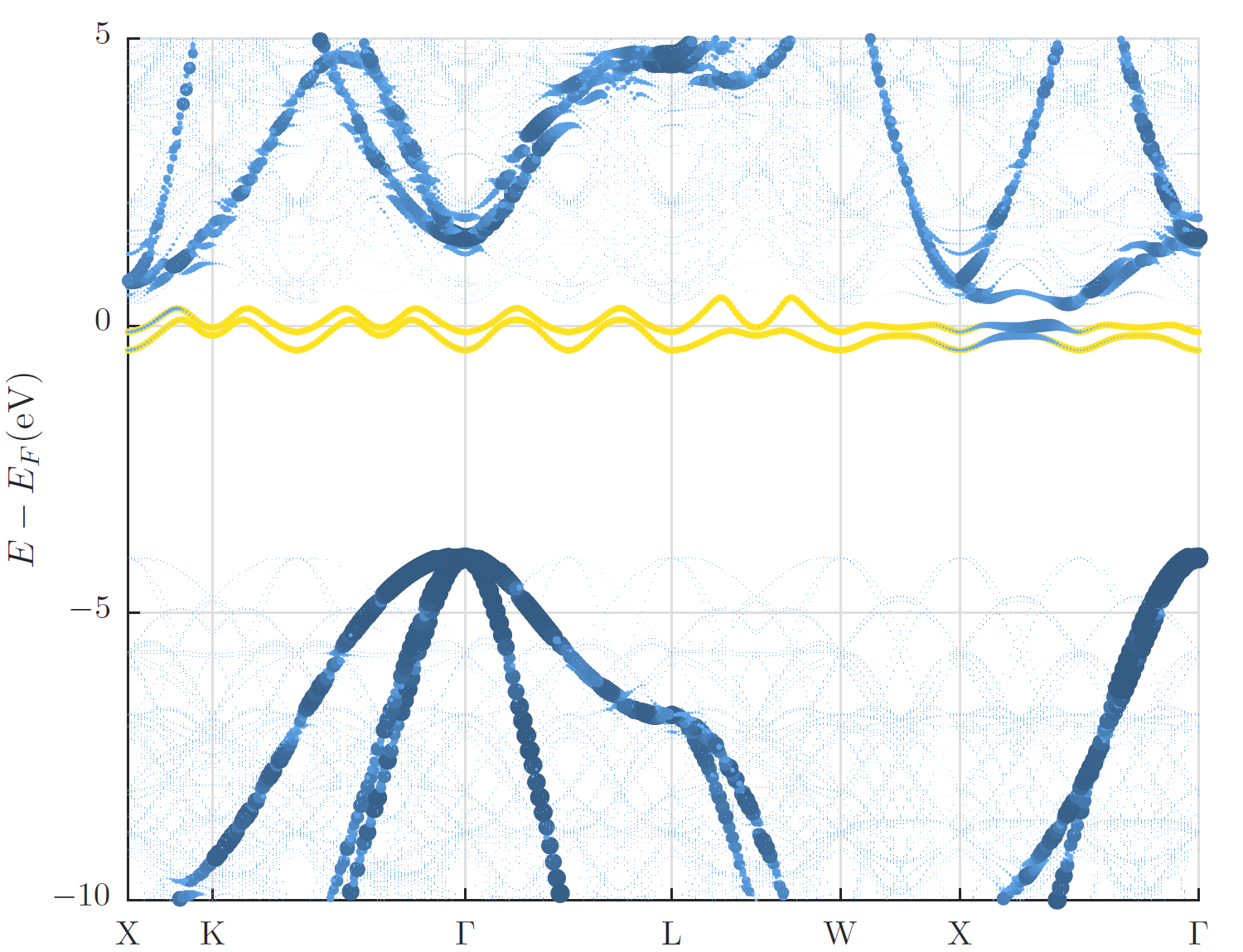
In the figure below the supercell band structure together with a visualization of the weights obtained for the backfolded band structure are shown along the -point path for the primitive unit cell. The visualization of the weights makes the backfolded band structure clearly identifiable while the supercell band structure is very faint. In addition to this visualization in the band gap the two defect states due to the A-nitrogen-center are highlighted in yellow.
Additionally the ability to use a rotated supercell is available. This can be useful for surfaces. The full tranformation matrix between the primitive cell and the supercell can be given below the unfolding input (example: 90° rotation of sqrt(3) x sqrt(3) hexagonal lattice). It has to consist of integer values for the unfolding to work.
<unfoldingBand unfoldBand="T" supercellX="1" supercellY="1" supercellZ="1">
<transMat>
<row-1>-1 2 0</row-1>
<row-2> 2 -1 0</row-2>
<row-3> 0 0 1</row-3>
</transMat>
</unfoldingBand>
It is important to note that the k-point path is not adapted automatically to the supercell when using the full transformation matrix. This means the path has to be given in terms of the supercell coordinates - in the example above M is at (0.5, 0.5) and K is at (1.0, 0.0). This matrix is multiplied from the right to the vector of basis vectors of the parent unit cell (a1, a2, a3) to give the basis vectors of the supercell.
In the case of using the entries supercellX, supercellY, and supercellZ it is not necessary to adapt the k-point path to the supercell, rather the path of the primitive cell can be given as an input. If the supercell has the same ratio of basis vectors as the primitive cell the path is found automatically by the input generator.
It is also possible to use the unfolding method for the case of spin-orbit coupling in 2nd variation (l_soc="T"). In this case a second variation eigenproblem is solved and the resulting wavefunctions are used. The switch useOlap allows to control whether the overlap matrix for the basis functions is used or not. In the case of unfolding for the second variation wavefunctions this switch has to be set to false (useOlap="F").
<unfoldingBand unfoldBand="T" supercellX="4" supercellY="4" supercellZ="4" useOlap="F"/>
The unfolding method is also of high interest for the calculation of film systems and surface states. In this case the unfolding is either performed purely in the z-direction or combined with a transormation matrix to allow the setup of an efficient surface cell. To simplify the setup the flag &expert primCellZ=6.854 / in the input generator can be used. This flag has two different functionalities. In the case of a true film system film=T the vacuum is set accordingly, so that the unfolding works (an integer multiple of the primitive cell is required). For the case of a pseudo film system (3D periodic system with additional vacuum) the input generator checks if the cell is a multiple of the size of the primitive cell in z-direction. The size of the primitive cell is to be given in atomic units.
