Choosing good parallelization schemes
The efficient usage of Fleur on modern (super)computers is ensured by a hybrid MPI/OpenMP parallelization. The -point loop and the eigenvector problem are parallelized via MPI (Message Passing Interface). In addition to that, every MPI process can be executed on several computer cores with shared memory, using either the OpenMP (Open Multi-Processing) interface or multi-threaded libraries.
In the following the different parallelization schemes are discussed in detail and the resulting parallelization scaling is sketched for several example systems.
MPI parallelization
- The -point parallelization gives us increased speed when making calculations with large -point sets.
- The eigenvector parallelization gives us an additional speed up but also allows to tackle larger systems by reducing the amount of memory each MPI process uses.
Depending on the specific architecture, one or the other or both levels of MPI parallelization can be used.
-point parallelization
This type of parallelization is always chosen if the number of -points (K) is a multiple of the number of MPI processes (P). If is not an integer, a mixed parallelization will be attempted and M MPI processes will work on a single k-point, so that is an integer. This type of parallelization can be very efficient because the three most time-consuming parts of the code (Hamiltonian matrix setup, diagonalization and generation of the new charge density) of different points are independent of each other and there is no need to communicate during the calculation. Therefore this type of parallelization is very beneficial, even if the communication between the nodes/processors is slow. The drawback of this type of parallelization is that the whole matrix must fit in the memory available for one MPI process, i.e., on each MPI process sufficient memory to solve a single eigenvalue-problem for a single point is required. The scaling is good as long as many points are calculated and the potential generation does not become a bottleneck. The superideal scaling in the following figure is caused by caching effects.
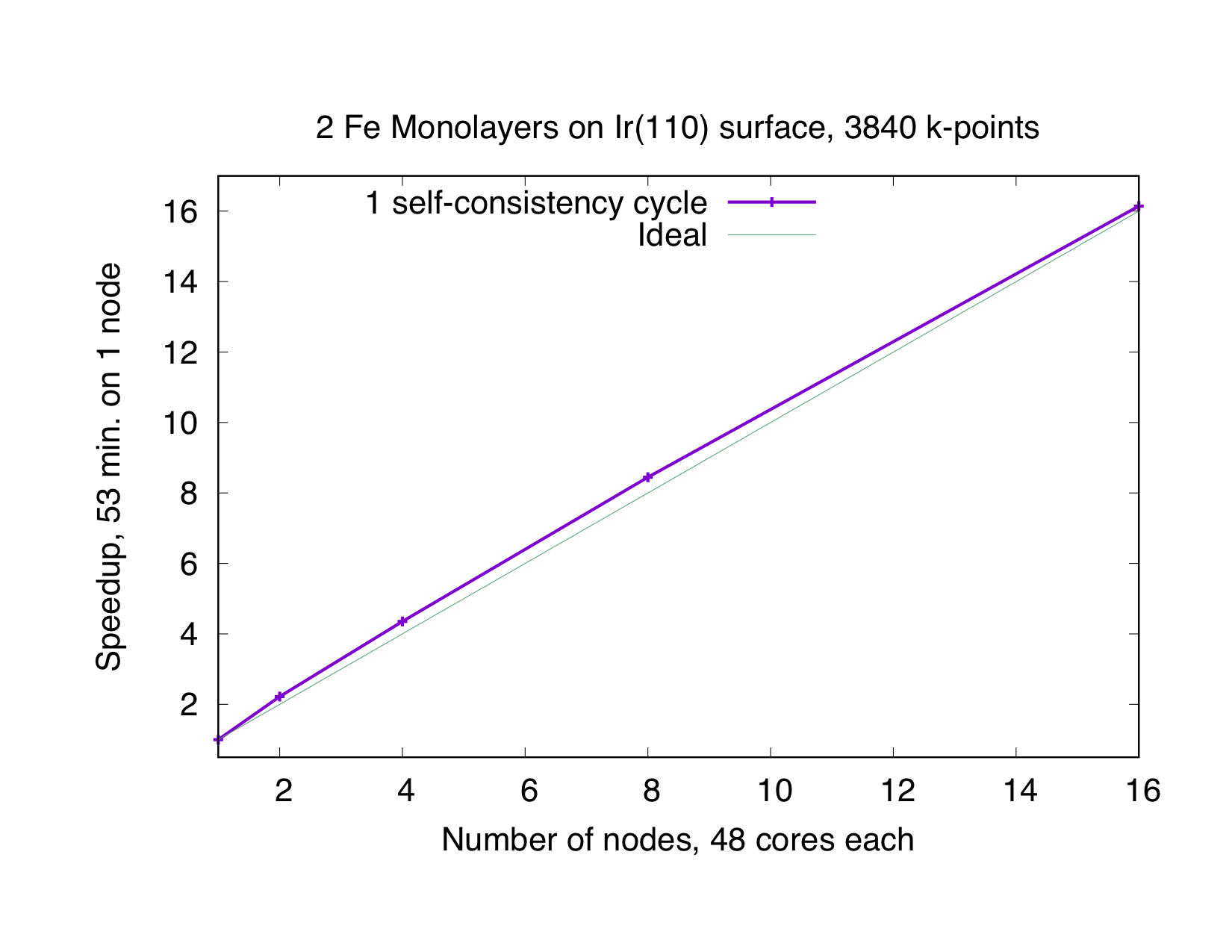
Eigenvector Parallelization
If the number of points is not a multiple of the number of MPI processes, every point will be parallelized over several MPI processes. It might be necessary to use this type of parallelization to reduce the memory usage per MPI process, i.e. if the eigenvalue-problem is too large. This type of parallelization depends on external libraries which can solve eigenproblems on parallel architectures. The Fleur code contains interfaces to ScaLAPACK, ELPA and Elemental. Furthermore, for a reduction of the memory footprint it is also possible to use the HDF5 library to store eigenvector data for each point on the disc. However, this implies a performance drawback.
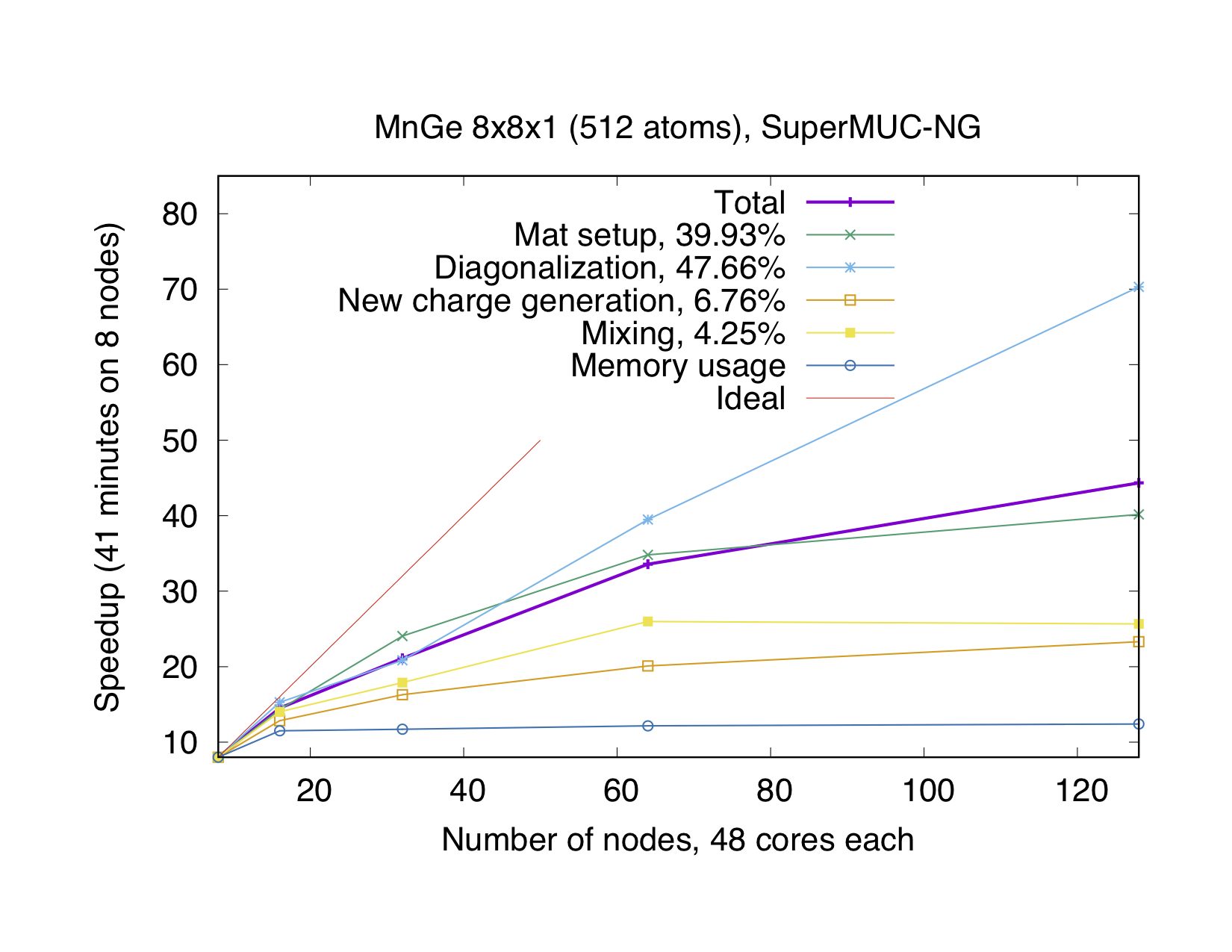
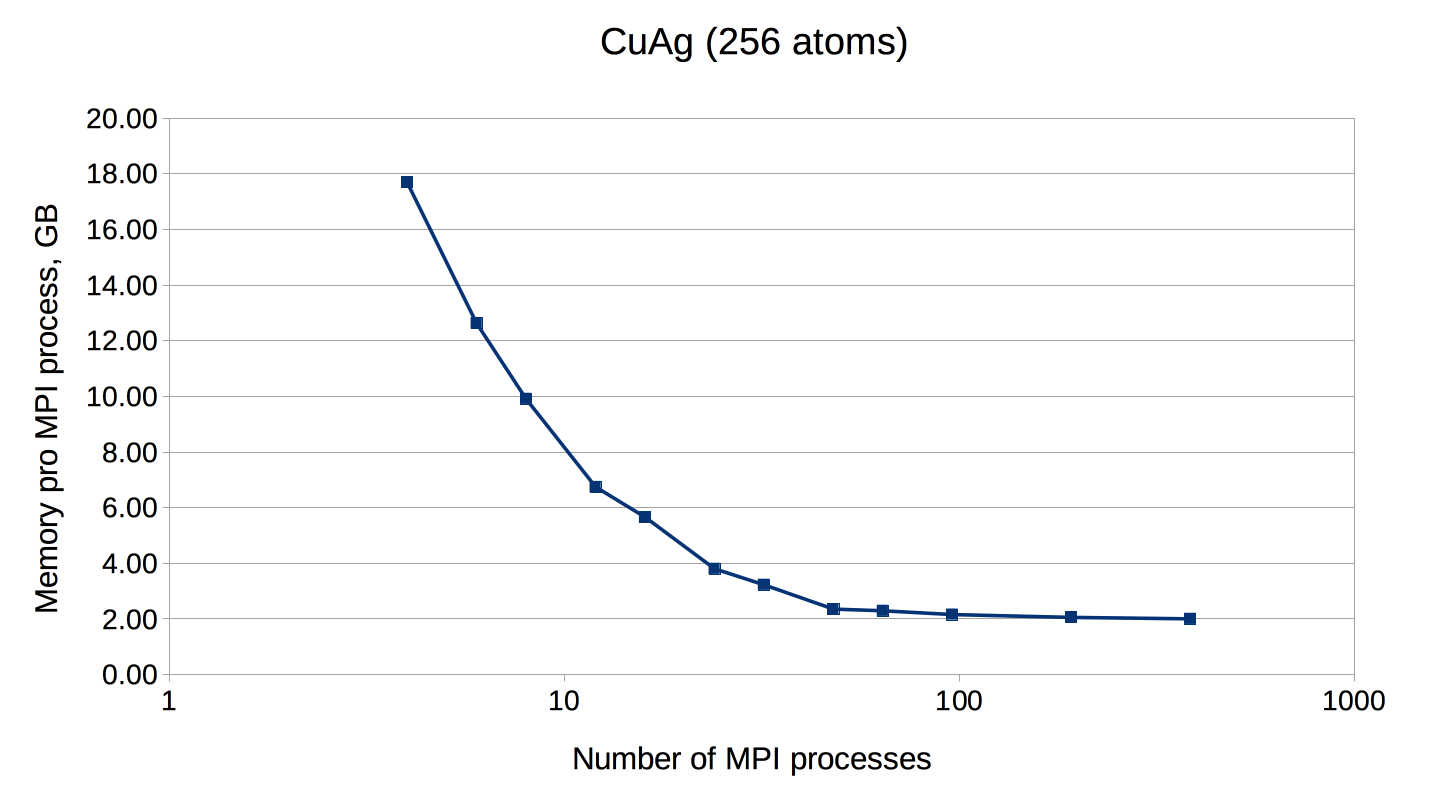
OpenMP parallelization
Modern HPC systems are usually cluster systems, i.e., they consist of shared-memory computer nodes connected through a communication network. It is possible to use the distributed-memory paradigm (MPI parallelization) also inside the node, but in this case the memory available for every MPI process will be considerably smaller. Imagine to use a node with 24 cores and 120 GB memory. Starting a single MPI process will make all 120 GB available to this process, two will only get 60 GB each and so on, if 24 MPI processes are used, only 5 GB of memory will be available for each of them. The intra-node parallelism can be utilized more efficiently when using the shared-memory programming paradigm, for example through the OpenMP interface. In the Fleur code the hybrid MPI/OpenMP parallelization is realised by directly implementing OpenMP pragmas and the usage of multi-threaded libraries. Note that in the examples above OpenMP parallelization was used together with the MPI parallelization. To strongly benefit from this type of parallelization, it is crucial that Fleur is linked to efficient multithreaded software libraries. A good choice is the ELPA library and the multithreaded MKL library. The following figure shows the pure OpenMP parallelization scaling on a single compute node.
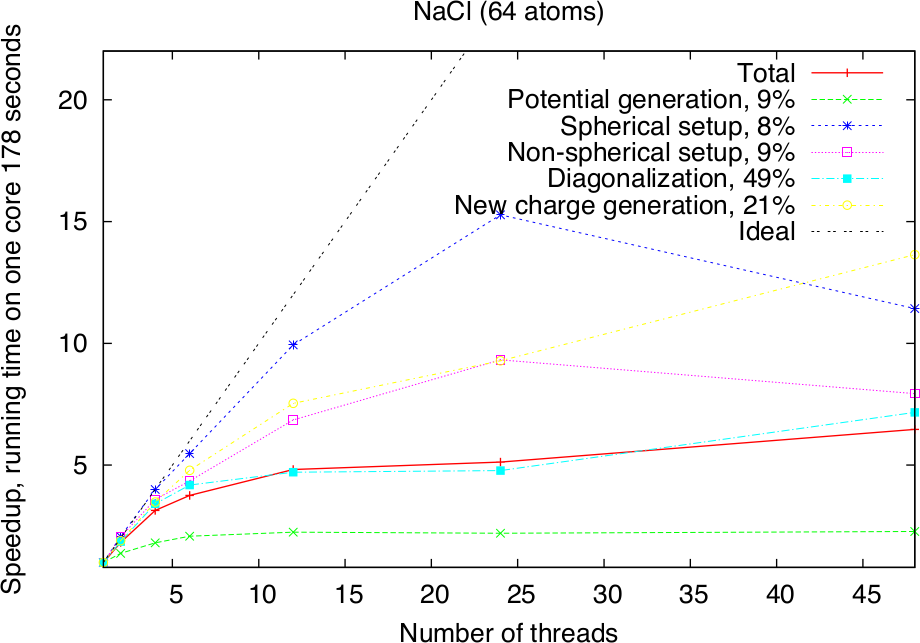
Parallel execution: best practices
Since there are several levels of parallelization available in Fleur: -point MPI parallelization, eigenvalue MPI parallelization, and multi-threaded parallelization, it is not always an easy decision how to use the available HPC resources in the most effective way: How many nodes are needed, how many MPI processes per node, how many threads per MPI process. A good choice for the parallelization is based on several considerations.
First of all, you need to estimate a minimum amount of nodes. This depends strongly on the size of the unit cell and the memory size of the node. In the table below some numbers for a commodity Intel cluster with 120 GB and 24 cores per node can be found - for comparable unit cells (and hardware) these numbers can be a good starting point for choosing a good parallelization. The two numbers in the "#nodes" column show the range from the "minimum needed" to the "still reasonable" choice. Note that these test calculations only use a single point. If a simulation crashes with a run-out-of-memory-message, one should try to double the requested resources. The recommended number of MPI processes per node can be found in the next column. If you increasing #k-points or creating a super-cell and you have a simulation which for sure works, you can use that information. For example, if you double #k-points, just double #nodes. If you are making a supercell which contains N times more atomes, than your matrix will be N-square times bigger and require about N-square times more memory.
Best values for some test cases. Hardware: Intel Broadwell, 24 cores per node, 120 GB memory.
| Name | # k-points | real/complex | # atoms | Matrix size | LOs | # nodes | # MPI per node |
|---|---|---|---|---|---|---|---|
| NaCl | 1 | c | 64 | 6217 | - | 1 | 4 |
| AuAg | 1 | c | 108 | 15468 | - | 1 | 4 |
| CuAg | 1 | c | 256 | 23724 | - | 1 - 8 | 4 |
| Si | 1 | r | 512 | 55632 | - | 2 - 16 | 4 |
| GaAs | 1 | c | 512 | 60391 | + | 8 - 32 | 2 |
| TiO2 | 1 | c | 1078 | 101858 | + | 16 - 128 | 2 |
The next question, how many MPI processes? The whole amount of MPI parocesses is #MPI per node times #nodes. If the calculation involves several points, the number of MPI processes should be chosen accordingly. If the number of points (K) is a multiple of the number of MPI processes (P) then every MPI procces will work on a given point alone. If is not an integer, a mixed parallelization will be attempted and M MPI processes will work on a single point, so that is an integer. This means for example that if the calculation uses 48 points, it is not a good idea to start 47 MPI processes.
As for the number of OpenMP threads, on the Intel architectures it is usually a good idea to fill the node with threads (i.e. if the node consist of 24 cores and 4 MPI processes are used, each MPI process should spawn 6 threads), but not to use the hyper-threading.
Example: Choosing the right parallelization on a single node
On a single Node using as much k-point parallelization is usually the most efficient parallelization. To get this you need to get the number of k-points in your calculation from your inp.xml or kpts.xml. Here we have a calculation with 20 k-points:
<kPointList name="default" count="20" type="tria-bulk">
We also need to know how many cores are on our node. In this example we will assume 12 cores. Then the number of MPIs is given by the greatest common denominator of 20 and 12:
n_mpi = gcd(12,20) = 4
n_openmp = n_cores / n_mpi = 12/4 = 3
Therefore we can start our calculation with:
export OMP_NUM_THREADS=3
mpirun -np 4 <insert your fleur binary here>
Further reading
- Parallelization and performance optimization: U. Alekseeva, G. Michalicek, D. Wortmann, and S. Blügel, Hybrid Parallelization and Performance Optimization of the FLEUR Code: New Possibilities for All-Electron Density Functional Theory. In: Aldinucci M., Padovani L., Torquati M. (eds) Euro-Par 2018: Parallel Processing. Euro-Par 2018. Lecture Notes in Computer Science, vol 11014. Springer, Cham.
- Parallelization of Hybrid functionals calculations with Fleur: M. Redies, G. Michalicek, J. Bouaziz, C., M. S. Müller, S. Blügel,and D. Wortmann, Fast All-Electron Hybrid Functionals and Their Application to Rare-Earth Iron Garnets, Front. Mater., 21 March 2022
